이번에 다뤄볼 주제는, 시그마($\sum$) :: 수열의 합입니다. 시그마를 잘 배워둔다면 앞으로 여러 가지 수열들의 합을 구할 때 흔히 말하는 하나하나 계산하는 과정 없이 공식만으로 아주 쉽고 편리하게 구할 수 있게 될 것입니다. 일단, 본론에 앞서, 처음 접하시는 분들은 시그마가 어려워 보이실 수 있는데, 절대 그렇지 않습니다! 잘 따라와 주세요.
시그마, 혹은 수열의 합의 정의: 수열 ${a_n}$의 첫째 항부터 제 $n$ 항까지의 합을 기호 $\sum$로 나타내고 합을 나타내는 영어의 Sum의 첫 글자 S에 해당하는 그리스 문자로, "시그마(sigma)"라고 읽는다. 표현: $a_1+a_2+a_3+\cdots+a_n = \displaystyle \sum_{k=1}^n a_k$
정의로만 보기에는 아직 낯섦이 있기에, '$2+4+6+8+10$'을 시그마로 나타내 봅시다:
$\displaystyle \sum_{n=1}^5 2n$
해석해보자면, n에 1부터 5까지 2n에 대입하여 더하는 것이라고 할 수 있습니다. 그래서, $\displaystyle \sum_{n=1}^5 2n$ = 2+4+6+8+10가 되는 것입니다. 슬슬 감이 오시죠? 다음으로, $\sum$의 기본 성질을 알아봅시다.
시그마도, 성립하는 연산법칙들이 있습니다.
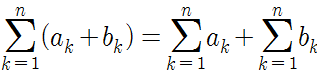
첫번째는, 시그마에 사용하는 일반항이 합으로 연결돼있다면, 이렇게 시그마 두 개로 분리할 수 있습니다. 어떻게 가능한지 간단하게 확인해봅시다.
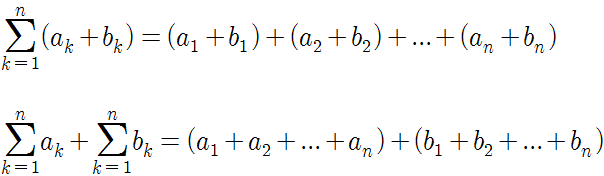
이렇게 나열해보니, 한 눈에도 보일 정도로 간단하게 정리가 됩니다. 덧셈은 교환 법칙이 성립하여, 계산 순서가 바뀌어도 성립하여
위의 두 식은 같다는 것을 알 수 있습니다.

둘째는, 분배 법칙에 해당하는 성질입니다.

이는 시그마의 일반항 부분에 있는 계수를 시그마 앞으로 묶어낼 수 있다는 것입니다. 이 역시, 나열해보면 쉽게 확인할 수 있습니다.

c가 모든 항에 대해 공통인수가 되기 때문에, 묶일 수 있어서, 시그마 앞으로 꺼낼 수 있게 되는 것입니다. 여기서 주의할 점은 상수가 아니고 k와 같이 상수가 아닌 변수라면 뺄 수 없습니다. k는 계속 변하는 변수이기 때문에, 성립하지 않기 때문입니다.
마지막으로, 일반항에 상수가 있는 경우입니다.
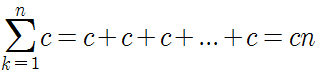
c는 변하지 않아 결국, 'c'를 n번 더하게 되어 $cn$이 되는 것입니다.
자, 지금까지 시그마의 정의, 성질을 알아보았습니다. 마무리 전, 시그마를 계산할 때 쓰게 될 시그마의 기본 공식들을 정리해 놓았습니다.
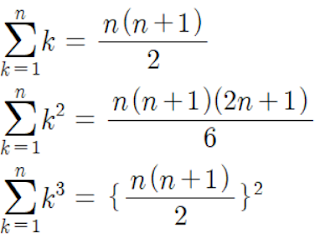
궁금한 내용이나 오류 제보 댓글로 남겨주세요! 감사합니다.
'MATH♪' 카테고리의 다른 글
| 페르마의 소정리 :: 증명하기 (0) | 2020.03.30 |
|---|---|
| 집합에 대한 모든 것 (I) :: 정의, 표현방법, 포함관계 (0) | 2020.02.27 |
| 등차수열 :: 기초부터 합 공식까지 다지기 (0) | 2020.02.23 |
| 인수분해 :: Factorization (0) | 2020.02.11 |
| 비둘기집 원리 :: Pigeonhole Principle (0) | 2020.01.27 |




